[AIVLE/Week2] 데이터와 친해지는 시간 - 파이썬 라이브러리, 데이터 처리, 데이터 분석 및 의미 찾기
Day4. Python 라이브러리
- 분석을 위한 데이터 구조
- 넘파이 기초
- 판다스 기초
에이블러들에게 매우 유명한 한기영 강사님 수업을 일주일 간 들었다. 수업을 듣기 전에도 기대가 컸지만! 조금 수업 듣다보니 역시나 정말 좋으신 분이구나~ 라고 생각이 들었다. 데이터 분석의 큰 그림을 접하고 데이터를 다루는 기초부터 넘파이, 파이썬 라이브러리까지 배웠다. 데이터의 관점에서 배열을 이해하고 헷갈리던 파이썬 기능들을 정리할 수 있었다.
<강의 정리>
✔ 너무 중요한 CRISP-DM(Cross-Industry Standard Process for Data Mining)
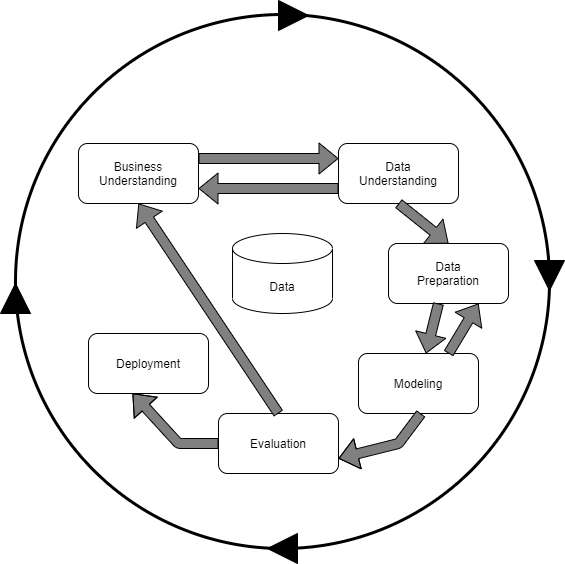
➡ 과제 수행의 기본 절차!
✔ 분석할 수 있는 데이터: 범주형(명목형, 순서형), 수치형(이산형, 연속형)
✔ 데이터에서 열: 정보, 변수, 요인, features, input
✔ 데이터에서 행: 분석단위, 샘플, 관측치, 데이터 건수, target
넘파이
✔ axis=0의 의미: 분석단위를 의미
✔ data.reshape(n, m(-1)) : 기존 데이터를 다른 형태의 데이터로 바꿔줌, n이 기존 데이터의 약수여야 함
✔ [:, n] :의 의미는 처음부터 끝까지!
✔ data[[행 조건], [열 조건]] : 필요한 행, 열 인덱스를 리스트 같은 자리로 받음
✔ 배열 사칙연산은 똑같은 위치끼리 계산함
✔ np.where(조건문, 참일 때 값, 거짓일 때 값)
판다스
✔ data.sort_values(by=기준 열, ascending=True(오른차순)) : 특정 열을 기준으로 정렬하기
✔ .unique() : 고유값 출력
✔ .value_counts() : 고유값과 그 개수 확인
✔ 특정 열 조회 : 여러 개 열을 조회하려면 꼭 리스트 안에 집어넣어야 한다! ex) df[['a', 'b']]
✔ .loc[행 조건, 열 이름(생략 가능)] : 단일 조건 조회
✔ 여러 조건을 연결할 때는 꼭! & 와 | 를 사용해야 한다. (안 그러면 에러남!)
✔ isin([값1, 값2, ..., 값n]) : 해당 값인 데이터만 조회. 꼭 리스트 형태로 input 값을 설정해야 한다.
✔ between(값1, 값2) : 값1 이상 값2 이하인 범위 내 데이터를 조회 (inclusive 조건에 따라 포함관계 설정 가능)
Day5. 데이터 처리
- 데이터 프레임 집계
- 데이터 프레임 변경
- 데이터 결합
파이썬 라이브러리 부분에서 어제 다 나가지 못한 부분을 배운 후 데이터 처리를 본격적으로 들어간 날이다. 다양한 함수들을 배우고 쓰는 법들을 익혔다. 실습을 병행하면서 배우다보니 확실히 사용법을 보다 수월하게 학습할 수 있었다. 그래도 복습은 정말 필수인가보다! 복습하는 지금 다시 보니 새삼 낯설게 느껴지기도.......
<강의 정리>
파이썬 라이브러리 - 데이터 프레임 집계
✔ data.groupby('A', as_index=)['B'].C : A 별 B 의 C 를 구한다.
- tip.groupby(’고객’, as_index = True)[[’tip’, ’price’]].sum() : 고객 별 가격과 팁의 합을 구해라.
✔ .agg(['sum', 'mean', 'max', 'min']) : 열 하나에 대한 합계, 평균 등 집계를 한 번에 수행 가능
데이터 처리
✔ 넓은 의미의 전처리: 데이터 구조 만들기 + 모델링을 위한 전처리
✔ 좁은 의미의 전처리: 모델링을 위한 전처리
➡ 모든 셀은 값이 있어야 함(결측치 처리)
➡ 모든 값은 숫자여야 함(가변수화)
➡ 필요시 숫자의 범위를 맞춰야 함(스케일링)
데이터 처리 - 데이터프레임 변경
✔ 열 이름 변경: df.columns / df.rename('이전 값' : '바꿀 값')
✔ 열 삭제: drop('열1' , axis=1, inplace=True) - 삭제할 열을 리스트 형태로 전달 시 여러 열 제거 가능
✔ 값 변경
- loc : ex) data2.loc[data2['Diff_Income'] < 1000, 'Diff_Income' ] = 0
- map() : ex) data['Gen'] = data['Gen'].map({'Male': 1, 'Female': 0})
- cut(조건, 구간 수) : 숫가형 변수를 범주형 변수로 변환, 값의 범위를 균등 분할(개수 균등 X)
1) 3 등분 분할 후 이름 붙이기 ex) age = pd.cut(data2['Age'], 3, labels = ['a','b','c'])
2) 내가 원하는 구간으로 자르기 ex) age = pd.cut(data2['Age'], bins =[0, 40, 50, 100] , labels = ['young','junior','senior'])
데이터 처리 - 데이터프레임 결합
- pd.concat() : 인덱스, 컬럼 이름이 기준. 합치려는 방향으로의 구조가 같아야 한다.
1) axis = 0 위아래로 합치기 / axis=1 옆으로 합치기
2) join = outer(합집합), inner(교집합)
- pd.merge() : 특정 컬럼의 값이 기준. 한 번에 두 개의 데이터프레임만 가능하다.
1) how = 결합 방식(left, right, inner, outer)
2) on = 결합 기준 열
- .pivot(index, column, values) : 집계된 데이터 재구성
Day6. 데이터 처리
- 시계열 데이터 처리
- 시각화 라이브러리
- 단변량 분석 - 숫자형 변수
- 단변량 분석 - 범주형 변수
데이터의 특성에 따라 적용할 수 있는 분석법을 배우는 것은 신기하고 유익하다!
+ 추가 정리. 오캄의 면도날이란? 무언가를 다양한 방법으로 설명할 수 있다면 우리는 그중에서 가장 적은 수의 가정을 사용하여 설명해야 한다는 뜻이다. 필요하지 않은 가정들은 잘라내자는 사고절약 원리가 담겨있다고 한다.
<강의 정리>
데이터 처리 - 시계열 데이터 처리
✔ 날짜 요소 추출: pd.to_datetime(date, format = '%d=%m-%Y')
✔ .shift() : 시계열 데이터에서 전후로 정보 이동. 설정한 기간만큼 정보 이동.
✔ .rolling().mean() : 시간의 흐름에 따라 일정 기간 동안 평균을 이동하면서 구함
✔ .diff() : 이전 시점 데이터와의 차이 구함
시각화 라이브러리 import matplotlib.pyplot as plt
✔ 기본차트 그리기 1️⃣plt.plot(data['Date'], data['Temp']) 2️⃣plt.plot('Date', 'Temp', data = data)
✔ 여러 그래프 겹쳐서 그리기 + 그 외 설정
plt.plot(data['Date'], data['Ozone'], label = 'Ozone') # label = : 범례추가를 위한 레이블값
plt.plot(data['Date'], data['Temp'], label = 'Temp')
plt.legend(loc = 'upper right') # 레이블 표시하기. loc = : 위치
plt.grid() # 그리드 추가
plt.xlabel('Date')
plt.title('Daily Airquality')
plt.xticks(rotation=45)
plt.show()
개별 변수(단변량)에 따른 사용 분석 도구 정리
| 그래프 | 통계량 | |
| 숫자 | 히스토그램, 밀도함수 그래프(Kde plot), 박스플롯 |
min, max, std, mean, 사분위수 |
| 범주 | bar plot(막대 그래프) | 범주별 빈도수 비율 |
단변량 분석 - 숫자형 변수
✔ 정보의 대푯값: 평균, 중위수, 최빈값, 사분위수 등
✔ 숫자형 변수 시각화
- 히스토그램 plt.hist(변수명, bins=), Kde plot sns.kdeplot(변수명), Box plot plt.boxplot(데이터, vert=)
- 적절한 bin 설정이 필요 (이상한 부분이 보이면 파고들어야 한다!)
- Box plot의 IQR: 1사분위 수 ~ 3사분위 수 까지의 범위
단변량 분석 - 범주형 변수
✔ 범주별 빈도수: 시리즈.value_counts()
✔ 범주별 비율: 범주별 빈도수를 전체 count로 나누기 data['column'].value_counts()/df.shape[0]
Day7. 데이터 분석 및 의미 찾기
- 단변량 종합 실습
- 이변량 분석 - 숫자 ➡ 숫자
- 이변량 분석 - 범주 ➡ 숫자
본격적으로 두 데이터 간의 관계를 파악하고 적절한 분석법을 택하는 법을 배웠다. 통계학적으로도 알아야할 게 참 많은 것 같다. 아직 헷갈리는 것들은 여러 번 다시보고 또 공부가 필요할 듯 싶다.
<강의 정리>
두 변수의 관계 분석(이변량 분석) - 숫자 ➡ 숫자
- 시각화) 산점도: 두 숫자형 변수의 관계를 나타내는 그래프(직선 관계 파악)
- 수치화) 상관계수, 상관분석
-1, 1에 가까울 수록 강한 상관관계를 나타냄
- p-value: 두 변수의 관계를 수치화한 값이 유의미한 지 판단하는 숫자(=유의확률)
p-value < 0.05이면, 두 변수 간에 관계가 있다고 여김. (= 상관계수가 의미가 있다.)
수치화: 상관계수의 한계
도구의 결과를 보고 단정적으로 파악하지 않는 것이 중요. 결과 부분 부분 속에 다양한 결과가 숨어있을 수 있음.
# matplotlib
plt.scatter('x', 'y', data=df)
# seaborn
sns.scatterplot('x', 'y', data=df)
# 상관계수
spst.pearson(df['x'], df['y'])두 변수간의 관계 분석(이변량 분석) - 범주 ➡ 숫자
1. 평균 비교 - barplot
barplot에서의 신뢰구간(오차범위) 의미: 평균값이 얼마나 믿을 만 한가?
- 좁을 수록 믿을 만 하다.
- 데이터가 많을수록, 편차가 적을 수록 신뢰구간은 좁아 짐
2. 범주 2개 : 두 평균의 차이 비교 - t-test
t-통계량이란? 두 그룹의 평균 간 차이를 표준오차로 나눈 값(=두 평균의 차이)
t 통계량, p-value 값을 구할 수 있음
3. 범주가 3개 이상 : 전체 평균과 각 범주의 평균 비교 = anova
- 여러 집단 간의 차이를 비교할 수 있다.
- 주의
분산분석은 전체 평균대비 각 그룹간 차이가 있는 지만 알려준다. 어느 그룹 간에 차이가 있는 지는 알 수 없다.
그래서, 통계 분야에서는 보통 사후분석을 진행한다. → anova 확인 후 각 그룹 간 두 그룹 씩 t-test
import scipy.stats as spst
spst.ttest_ind(B, A, equal_var=False) # t-test
spst.f_oneway(group a, group b, group c) # anovaDay8. 데이터 분석 및 의미 찾기
- 이변량 분석(숫자) 종합 실습
- 이변량 분석 - 범주 ➡ 범주
- 이변량 분석 - 범주 ➡ 숫자
데이터 분석 및 의미 찾기 과목의 마지막 날! 계속해서 강사님께서 총 정리를 해주시고, 최대한 쉽게 알려주셔서 잘 따라올 수 있었다.
<강의 정리>
이변량 분석 - 범주 ➡ 범주
1. 일단 crosstab 그리기
pd.crosstab(행: titanic['Survived'], 열: titanic['Sex'], 비율 출력 여부: normalize='columns')
2. 교차표로부터 시각화와 수치화를 수행
- 시각화 (mosaic plot), 수치화(카이제곱 검정)
<범주 ➡ 범주 시각화: mosaic plot>
- 코드: mosaic(data, [범주형 컬럼, 범주형 컬럼])
- 빨간 선은 전체 평균을 의미
- x축의 길이는 각 범주 별 비율을 나타낸다.
- 두 범주형 변수가 아무런 상관이 없다면 전체 평균 비율과 범주 별 각 평균이 같을 것
<범주 ➡ 범주 수치화: 카이제곱검정>
- 카이제곱 통계량이란: 기대빈도와 실제 데이터와의 차이
- 값이 클 수록 기대빈도로부터 실제 값에 차이가 큼
- 범주의 수가 늘어날 수록 값은 커지게 되어 있다.
- 자유도의 약 2배 보다 크거나 p-value가 0.05 이하면 차이가 있다고 본다.
자유도란? 범주의 수 - 1
카이제곱 검정에서는 (x 변수의 자유도) * (y 변수의 자유도)로 계산한다.
- 코드: crosstab으로 집계 후 해당 table을 통해 구함. 이때 crosstab에 normalize 옵션을 적용하면 안 됨.
spst.chi2_contingency(table)
이변량 분석 - 숫자 ➡ 범주
시각화: kde plot
둘 사이에 관련이 없다면 범주에 따른 그래프가 완전 일치할 것: 겹치는 곳은 전체 평균과 일치하는 지점이기 때문
분석방법 정리
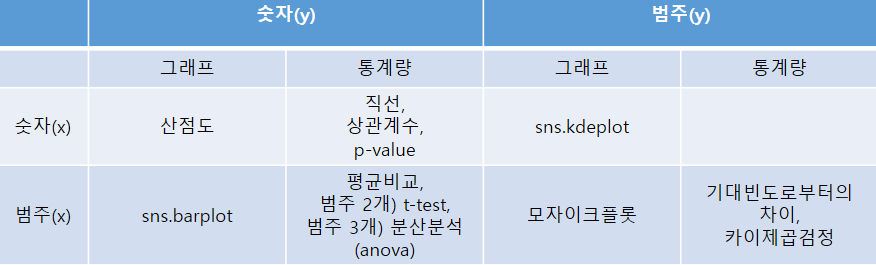

예... 기자단하면 부지런히 복습하고 공부 블로그하는 사람이 될 거라 기대했지만 역시나 그냥 블로그 밀린 게으름뱅이가 되었다. ㅋㅋㅋㅋㅋㅋㅋㅋ 그래도 이렇게 다시 복습하니까 새록새록 기억이 나고 한 번 다시 정리해서 너무 다행이다라는 생각이 든다! 약 두 달차가 되어가는데 차곡차곡 배워왔구나 새삼 깨닫고,,, 더 밀리기 전에 부지런히 복습 따라가보겠다. 💪